Brief analysis of the faint source HLS091828 (z=5.243)
Coordinates:
- R.A. = 09h18m28.6s
- Dec. = 51d42'23.3"
Expected fluxes (Combes et al. 2012):
- F0.88mm= 125+-8mJy
- F1.3sma= 55+-7mJy
- F2mm= 15+-7mJy
NIKA obsevations:
Day: 13/06/2013
Scans: 9 Lissajous of 5 min (<=> 45 min) each with followed by tracks (for tuning), 180 to 197
Size of the map:90"x90"
Opacity at 225 GHz: 0.7-0.8
Elevation of the source: ~50 deg
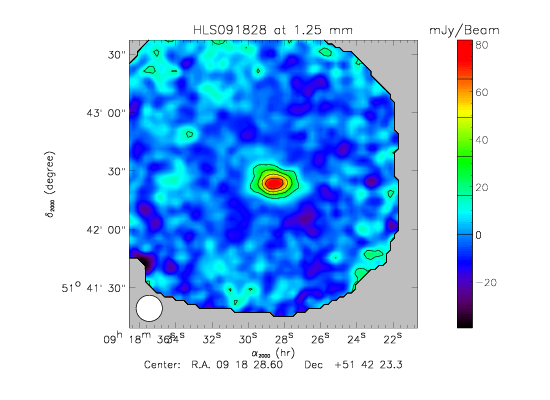
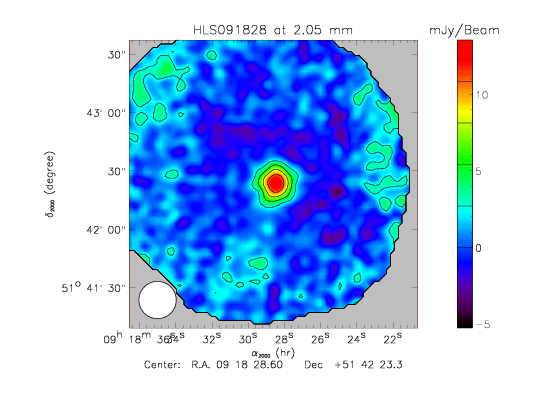
- We detect the source at both wavelenghts, shown on the maps given bellow. The standard deviation of the Jack-Knife map gives the noise level:
- ~8 mJy/Beam at 1mm
- ~1 mJy/Beam at 2mm
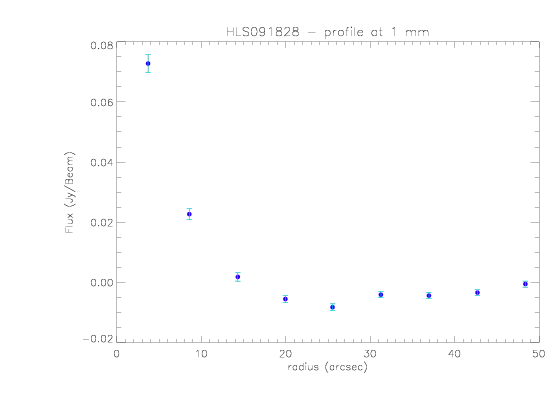
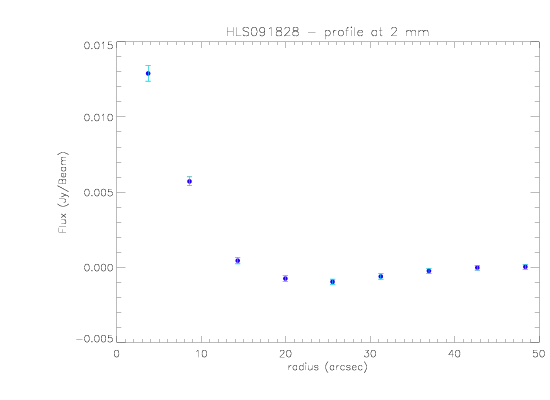
Profiles:
- The profiles are computed by averaging the map in concentric annuli, and we check that the measured flux is, a priori, consistent with what we expect at 2mm but too high at 1mm.
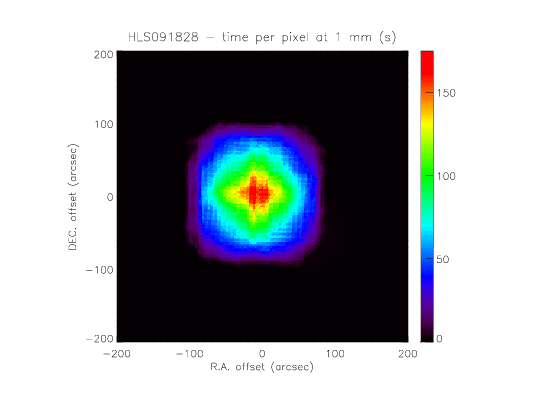
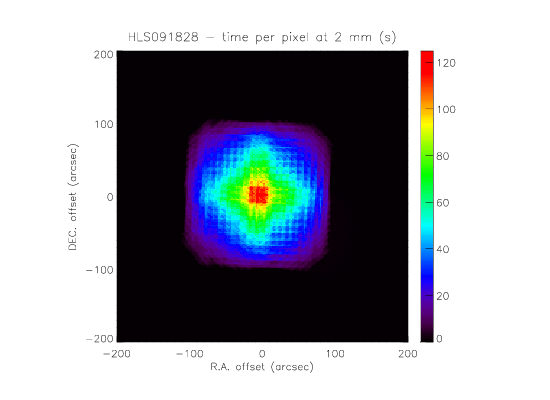
Time per pixel:
- The time per pixel maps are also shown. It is equivalent to the number of hit map, divided by the sampling frequency. The pixels are 2"x2" here.
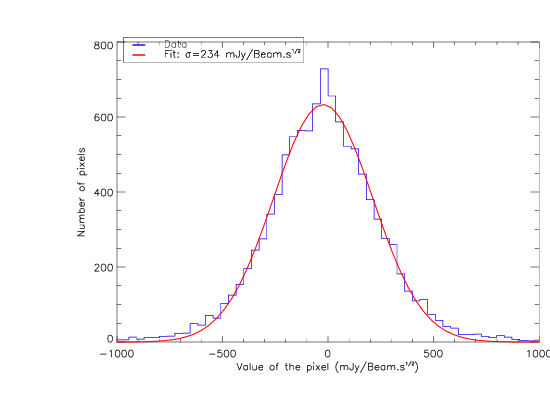
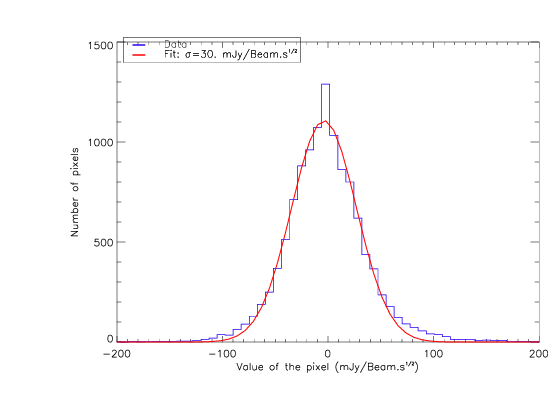
Noise estimates:
- By multiplying the Jack-Knife maps with the square root of the time per pixel maps and computing the histogram of the obtained map, we are able to estimate the noise level in the data. Note that this is in the case of high opacity (we can expect the noise to be reduced by a factor of about exp(-tau/sin(elevation)) ~ 2, and even more since the resonances are larger under large optical load), and at 1mm it might even be reduced again by a factor of ~2 since we are apparently over calibrated.
- If this is correct, the noise is:
~50 mJy/Beam.sqrt(s) at 1mm
~15 mJy/Beam.sqrt(s) at 2mm
- We can estimate the noise on the Jack-Knife maps directly. With the raw map (2"x2" pixels, not filtered), we obtain at the at center of the map:
- 42 mJy/Beam at 1mm
- 6 mJy/Beam at 2mm
- If we smooth the map with a gaussian filter with FWHMs equals the the respective beams, we get:
- 3.4 mJy/Beam at 1mm
- 0.3 mJy/Beam at 2mm
- Since the array (i.e. the source is always seen by a detector) is always on-source, the sensitivity might be estimated to be:
- 3.4 x sqrt(45 min) = 180 mJy/Beam.sqrt(s)
- 0.3 x sqrt(45 min) = 15.6 mJy/Beam.sqrt(s)